18.2 菱形(性质)
莫旗教研培训中心 戴常福
教材分析
课标要求:
1.理解“菱形”的概念,明确“菱形”与“平行四边形”之间的关系.
2.探究并证明菱形的性质定理.
地位作用:本节内容是本章内容前后衔接的关键,也是渗透由一般到特殊研究几何知识方式方法的一个样板,菱形性质的证明过程是对学过的知识一次很好的综合应用。在后续的几何学习过程中,菱形性质也是运用频率较高的依据。
编者意图分析
教材先通过一个动态的图示明确了菱形的概念,形成的概念不是死的,而是一个鲜活的过程,与矩形和后面的正方形的学习一起展现给学生的是一种用运动变化的思维研究几何知识的方法。概念明确以后,例举几个实例,又给学生留有联想空间,意在感受知识与生活实际的密切联系,也是强化概念的一个很好过程。思考栏,不仅仅提出了新的思考任务,同时也渗透了发现问题和提出问题的方法。后续又一次提示探究菱形性质的着眼点,是又一次方式方法的渗透。性质得出后,证明留白,给学生留有足够的尝试空间。由对角线求菱形面积和菱形的轴对称性虽没以黑体字方式给出,但也是菱形重要的性质,教材中分别以书签和补充阅读的形式给予明确。例题的选材是与学生生活非常近的实例,即能很好的起到巩固新知的作用,又能让学生感受到书本知识来源于生活又服务于生活的事实,能起到较好的激趣作用。课后配备的习题虽难度不大,但针对性很强,又富有变式的空间。
学情分析
初二的学生对菱形并不陌生,在前面的学习中,对其早已有了初步的感性认识。在具体的性质探究上又有刚刚对矩形性质探究的经历,积累了一定的由一般到特殊研究特殊四边形经验,所以应该比较容易。在性质证明时需要用到等腰三角形的有关性质,因为时间间隔较长,应该略有难度。
教学目标
1.理解菱形的概念. 明确菱形与平行四边形的联系与区别.
2.探究并证明菱形的相关性质,并能灵活运用.
3. 通过观察由平行四边形到菱形的转化过程和对菱形性质的探究过程, 学习由一般到特殊的探究几何知识的方式方法.
4. 在知识的探究过程中,培养学生与他人交流的能力和意愿.
教学重点
理解菱形的概念.掌握菱形的性质.
教学难点
1. 菱形性质的灵活运用.
2. 利用对角线求菱形面积公式的推导和归纳.
教法学法
教师:明确任务,提供学具,提供充足的探究空间和交流的时间,适时 点拨引导,使学生对新知的认识逐层递进,直至清晰。
学生:先独立思考,适时合作,借鉴他人智慧完善自己的知识体系。
教学准备: 多媒体,ppt课件
教学过程
活动一:3分钟
由回顾矩形的形成过程直接过度到特殊平行四边形的另一种情形(邻边相等),明确菱形概念。
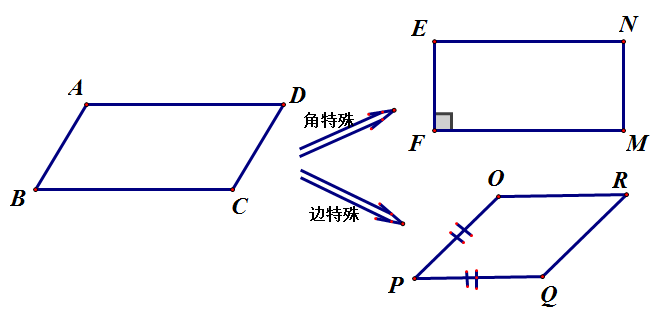
设计意图:利用几何画板动画演示,在变化的过程中,更能凸显“特殊”的含义,更容易建立完整的概念。
活动二:2分钟
菱形实物的举例,强化对概念的理解,感受数学知识与生活的密切联系。




设计意图:构建生活经验与书本知识的联系。培养学以致用的意识。这段过度意在引导学生学习用类比的方式思考问题,解决问题。
活动三:15分钟
在矩形的学习过程中,我们已经知道作为特殊的平行四边形的矩形,除具有平行四边形的一切性之外,还有一些属于自己的特有性质,菱形也是特殊的平行四边形,它又有哪些属于自己的性质呢?
让我们先来动手制作一个探究新知的素材,凭着自己对菱形概念的理解,把老师发到各小组的平行四边形卡纸进行加工,使之成为一个菱形(比一比,哪一个小组的方法最巧妙)。
借助于上面自己做得的菱形卡片,寻找菱形的特有性质吧,比一比我们谁是火眼金睛,谁更善于推理,看看哪个小组找到的最多。(视学生实际情况,如果进行的不顺利,可以提示寻找性质的着眼点,如果顺畅就完全放手。鼓励学生不要满足于既得成果,要善于求异求变)
希望得到的结论有:
1.菱形的四条边相等.
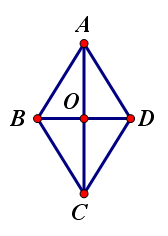
2.菱形的对角线互相垂直,并且每一条对角线平分一组对角.
3.被对角线分得的四个三角形是四个全等的直角三角形.
4.菱形是以对角线为对称轴的轴对称图形.
设计意图:在动手操作过程中再次加深对菱形的认识,也为性质的寻找做一个铺垫。借助于课堂评价,充分调动起学生的参与热情,以小组为单位评价目的是强行锻炼学生与他人交流的意愿和能力,进而培养良好的合作意识。哪个小组找到的多由哪个小组汇报,然后相互补充,达成共识后在有学生一一说明理由,性质二作为重点,规范板书。
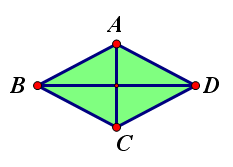
活动四:7分钟
5.如图,四边形ABCD是菱形,对角线AC,BD相交于点O,且AC=8,BD=6.试求菱形ABCD的周长和面积. (找到解决方法后,把已知条件改成AC = a,BD=b, 求菱形ABCD的面积,然后对所得结果加以提炼,得到菱形特有的面积求法。)
设计意图:对刚刚得到的知识的运用,同时又是从特殊到一般探究知识方法的渗透。
活动五:10分钟
如图,四边形ABCD是一个菱形的花坛,沿对角线修建了两条小路AC和BD,C=10m,∠ABC=60°.求另一条对角线的长和花坛的面积.(视情况进行一些简单的拓展练习和变式训练)
设计意图:对本节课探究所得的综合应用,对例题的简单变式是为了避免直接照搬式的完成。
活动六:6分钟
当堂检测:
如图,四边形ABCD是菱形,AC,BD相交于点O,∠ACD=30°,BD=6.
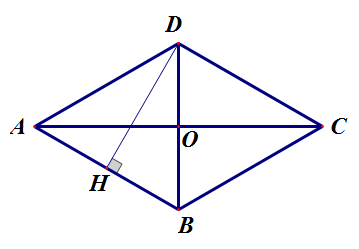
求:① ∠BAD和 ∠ABC的度数.
② AC的长和菱形ABCD的周长.
③ 求菱形ABCD的面积.
④ 求AB边上的高DH的长。
设计意图:进一步巩固新知,检查学生对新知掌握情况的同时,在第4问也增加了难度,意在为优等生提供足够的挑战。第4小问可以采用多种方法,锻炼学生综合运用所学知识的能力,又可激发学生探究几何问题得兴趣。
活动八:2 分钟
小结:
1.知识收获:
2.方法收获:
3.存在的困惑或新的猜想:
作业 60页, 第5题;61页,第10题,第11题.
板书设计 课题:18.2.2 菱形(性质)
性质: 投影: 例题:

